PULAU KEMARO

Pulau Kemaro adalah salah satu juara wisata di Palembang. Terletak di Ilir Sungai Musi, pulau ini memiliki luas 5 hektare. Ada sebuah pagoda indah di dalam pulau yang selalu ramai setiap perayaan Cap Go Meh atau malam ke-15 setelah Imlek. RIbuan orang berdatangan untuk merayakan sekaligus berwisata ke pulau religius ini.

       Pulau Kemaro identik dengan kaum Tionghoa. Pulau ini akan sangat ramai dikunjungi pada saat perayaan Imlek dan Cap Go Meh. Daya tarik utama pulau ini adalah sebuah pagoda berlantai sembilan yang pada saat malam hari berhiaskan cahaya lampu yang sangat menawan. Ada sebuah legenda yang terkenal mengenai Pulau Kemaro. Pulau yang berada di tengah-tengah sungai Musi ini menyimpan kisah cinta antara Tan Bun An, seorang pangeran dari negeri Cina,  dengan Siti Fatimah, seorang putri Sultan Palembang. Kisah ini terjadi di masa pemerintahan Sultan Palembang pada tahun 1706-1714M. Alkisah Tan Bun An hendak melamar Siti Fatimah. Tan Bun An diperbolehkan melamar sang putri asalkan mampu memberi mas kawin tujuh guci berisi emas. Ayah Tan Bun An kemudian mebawakannya puluhan guci untuk bekal anaknya melamar putri Palembang. Tan Bun An kembali ke Palembang dengan membawa puluhan guci yang dibawakan ayahnya. Tan Bun An mengira bahwa dalam puluhan guci terebut berisi emas, jadi bukan hanya tujuh seperti yang diminta sang putri.  Namun ia tidak tahu bahwa ayahnya hanya membawakan tujuh guci emas, guci-guci lainnya hanyalah berisi sayur yang dimaksudkan untuk mengelabui bajak laut yang sering mengganggu jalur pelayaran. Tujuh guci yang berisi emas itu pun ditutupi dengan sayuran diatasnya.

       Pada saat kapal Tan Bun An telah tiba di sungai Musi, Tan Bun An hendak memeriksa guci-guci tersebut, alangkah terkejutnya Tan Bun An begitu mengetahui bahwa isinya bukanlah emas, namun sayuran! Karena merasa malu, Tan Bun An kemudian membuang  guci-guci tersebut ke sungai Musi, ketika guci terakhir dibuang, guci tersebut jatuh di badan kapal dan pecah, kemudian berhamburanlah emas yang dibawakan keluarga Tan Bun An.

Sadar bahwa ada 6 guci lain berisi emas yang sudah terlanjur dibuang, Tan Bun An beserta pengawalnya kemudain terjun ke Sungai Musi untuk mencari guci yang terlanjur dibuang, namun mereka tak juga muncul ke permukaan. Siti Fatimah yang sudah jatuh cinta merasa sedih dan kemudian ikut terjuan menyusul Tan Bun An ke Sungai Musi. Sebelumnya Siti Fatimah berpesan apabila dia tidak berhasil menemukan Tan Bun An dan bila suatu hari ada gundukan tanah yang muncul, maka disanalah kuburan sang putri. Setelah lama sang putri tak muncul ke permukaan, kemudian muncullah gundukan tanah yang sekarang menjadi Pulau Kemaro.

     Suasana Pulau Kemaro sendiri saat ini sangat teduh dengan banyak pohon-pohon besar yang menaunginya sehingga Pulau Kemaro juga berfungsi sebagai paru-paru kota. Pohon besar dibawah ini dipercaya sebagai pohon lambang cinta, bagi mereka yang meminta jodoh disini pasti akan mendapat jodoh (konon kabarnya begitu).

GELOMBANG

<> Pengertian Gelombang

        Gelombang adalah bentuk dari getaran yang merambat pada suatu medium. Pada gelombang yang merambat adalah gelombangnya, bukan zat medium perantaranya. Satu gelombang dapat dilihat panjangnya dengan menghitung jarak antara lembah dan bukit (gelombang tranversal) atau menghitung jarak antara satu rapatan dengan satu renggangan (gelombang longitudinal). Cepat rambat gelombang adalah jarak yang ditempuh oleh gelombang dalam waktu satu detik.

      Gelombang didefinisikan sebagai getaran yang merambat melalui medium, berupa zat padat, cair, dan gas. Gelombang adalah getaran yang merambat. Bentuk ideal dari suatu gelombang akan mengikuti gerak sinusoide. Selain radiasi elektromagnetik, dan mungkin radiasi gravitasional, yang bisa berjalan lewat vakum, gelombang juga terdapat pada medium (yang karena perubahan  bentuk dapat menghasilkan gaya memulihkan yang lentur) di mana mereka dapat berjalan dan dapat memindahkan energi dari satu tempat kepada lain tanpa mengakibatkan partikel medium berpindah secara permanen; yaitu tidak ada perpindahan secara masal. Malahan, setiap titik khusus berosilasi di sekitar satu posisi tertentu.

      Berdasarkan medium perambatannya, gelombang dikelompokkan menjadi dua, yaitu gelombang mekanik dan gelombang elektromagnetik. Gelombang mekanik yaitu gelombang yang memerlukan medium di dalam perambatannya. Contoh gelombang mekanik antara lain: gelombang bunyi, gelombang permukaan air, dan gelombang pada tali. Gelombang elektromagnetik adalah gelombang yang tidak memerlukan medium dalam perambatannya. Contoh : cahaya, gelombang radio, gelombang TV, sinar – X, dan sinar gamma.

1. Gelombang Mekanik

      Gelombang terjadi karena adanya usikan yang merambat. Menurut konsep fisika, cerminan gelombang merupakan rambatan usikan, sedangkan mediumnya tetap. Jadi, gelombang merupakan rambatan pemindahan energi tanpa diikuti pemindahan massa medium. Berdasarkan arah rambat dan arah getarnya, gelombang dibedakan atas gelombang transversal dan gelombang longitudinal. 

A. Gelombang Transversal 

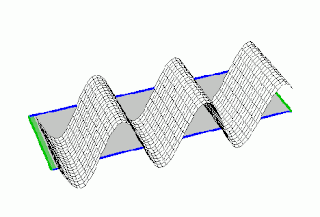
   Gelombang transversal adalah gelombang yang arah rambatnya tegak lurus dengan arah getarnya. Satu gelombang terdiri atas satu lembah dan satu bukit, misalnya seperti riak gelombang air, benang yang digetarkan, dsb.

 Klik gambar untuk lihat animasinya

Contoh gelombang transversal :

- getaran sinar gitas yang dipetik.

- getaran tali yang digoyang-goyangkan pada salah satu ujungnya.

 

B. Gelombang Longitudinal

        Gelombang longitudinal adalah gelombang yang merambat dalam arah yang berimpitan dengan arah getaran pada tiap bagian yang ada. Gelombang yang terjadi berupa rapatan dan renggangan. Contoh gelombang longitudinal seperti slingki / pegas yang ditarik ke samping lalu dilepas.

Perhatikan ilustrasi berikut ini !

Contoh gelombang longitudinal :

1. Gelombang pada slinki yang diikatkan kedua ujungnya pada statif kemudian diberikan usikan pada salah satu ujungnya.

2. Gelombang bunyi di udara

C.  Panjang Gelombang

Panjang satu gelombang sama dengan jarak yang ditempuh dalam waktu satu periode.

1. Panjang gelombang dari gelombang transversal

         Pada gelombang transversal, satu gelombang terdiri atas 3 simpul dan 2 perut. Jarak antara dua simpul atau dua perut yang berurutan disebut setengah panjang gelombang atau ½ λ (lambda).

2.  Panjang gelombang dari gelombang longitudinal

       Pada gelombang longitudinal, satu gelombang (1l) terdiri dari 1 rapatan dan 1 reggangan.

D. Cepat Rambat Gelombang

        Jarak yang ditempuh oleh gelombang dalam satu sekon disebut cepat rambat gelombang. Cepat rambat gelombang dilambangkan dengan v dan satuannya m/s atau m s^-1. Hubungan antara v, f, λ, dan T adalah sebagai berikut :

Keterangan :

λ= panjang gelombang , satuannya meter ( m )

v = kecepatan rambatan gelombang, satuannya meter / sekon ( ms^-1 )

T = periode gelombang , satuannya detik atau sekon ( s )

f = frekuensi gelombang, satuannya 1/detik atau 1/sekon ( s^-1 )

E. Gelombang menurut amplitudo dan fasenya 

1. Gelombang berjalan

         Gelombang berjalan adalah gelombang yang amplitudo dan fasenya sama di setiap titik yang dilalui gelombng. Amplitudo pada tali yang digetarkan terus menerus akan selalu tetap, oleh karenanya gelombang yang memiliki amplitudo yang tetap setiap saat disebut gelombang berjalan.
Misalkan seutas tali kita getarkan ke atas dan ke bawah berulang-ulang seperti pada Gambar disamping ini. Titik P berjarak x dart titik 0 (sumber getar), Ketika titik 0 bergetar maka getaran tersebut merambat hingga ke titik P,Waktu yang diperlukan oleh gelombang untuk merambat dari titik o ke titik P adalah x / v dengan demikian bila titik 0 telah bergetar selama t detik maka titik p telah bergetar selama tP dengan.

t_p= t- x/v 

Berdasarkan uraian diatas maka akan didapatkan persamaan simpangan gelombang, sebagai berikut: 

y=A sin 2λ/T t

         Persamaan simpangan di titik P dapat diperoleh dengan mengganti nilai t dengan tp sehingga kita dapatkan hubungan berikut. 

yp=A sin 2λ/T (t-x/v)

Keterangan :

A = amplitudo gelombang (m)

T = periode gelombang (s)

t = lamanya titik 0 (sumber getar) bergetar (s)

x = jarak titik P dari sumber getar (m)

v = cepat rambat gelombang (m/s)

yp= simpangan di titik P (m)

             dalam hal ini gelombang memiliki dua kemungkinan dalam arah rambatannya, oleh karenanya perlu diperhatikan langkah sebagai berikut:

<> Apabila gelombang merambat ke kanan dan titik asal 0 bergetar ke atas maka persamaan simpangan titik P yang digunakan adalah: 

yp= A sin 2λ/T (t-x/v)

<> Apabila gelombang merambat ke kiri dan titik asal 0 bergetar ke bawah maka persamaan simpangan titik P yang digunakan adalah:

y_p = - A sin 2λ/T (t-x/v)

         Fase di definisikan sebagai perbandingan antara waktu sesaat untuk meninggalkan titik keseimbang (titik 0) dan periode. Dengan demikian fase gelombang dititik P dapat ditulis sebagai berikut:

φ = t_p/T

   = (t- x/v)/T                                            φ_p = t/T -  x/λ             

   = t/T- x/vT

Sehingga dihasilkan besarnya sudut fase di titik P dapat dituliskan sebagai berikut:

θp = 2π φ_p

     =2π (t/T- x/λ)

Beda fase antara dua titik yang berjarak X₂ dan X₁ dari sumber getar dapat dituliskan sebagai berikut:

Δφ  = ( x₂ - x₁)/λ

Δφ  =  ∆x/λ

Nilai kecepatan dan percepatan gelombang di suatu titik dapat diketahui dengan menurunkan persamaan keduanya, sebagai berikut:

v_p = 2π/T A cos 2λ/T (t-x/v)

ap= - (4π²)/T² A cos  2λ/T (t-x/v)

Keterangan:

vp = kecepatan partikel di titik p (m/s)

ap = percepatan partikel di titik p (m/s2)

'Contoh soal:

Suatu gelombang berjalan memiliki persamaan y = 10 sin (0,8πt - 0,5πx) dengan y dalam cm dan t dalam detik. Tentukanlah kecepatan dan percepatan maksimumnya!

Pembahasan:

y= 10 sin (0,8πt - 0,5πx)

v = dy/dt

v= (10)(0,8π) cos (0,8πt - 0,5πx)

nilai v maksimum bila cos (0,8πt - 0,5πx) = 1

2. Gelombang Stasioner (diam)

        Adalah gelombang yang memiliki amplitudo yang berubah – ubah antara nol sampai nilai maksimum tertentu. Gelombang stasioner dibagi menjadi dua, yaitu gelombang stasioner akibat pemantulan pada ujung terikat dan gelombang stasioner pada ujung bebas.

 

             Seutas tali yang panjangnya l kita ikat ujungnya pada satu tiang sementara ujung lainnya kita biarkan, setela itu kita goyang ujung yang bebas itu keatas dan kebawah berulang – ulang. Saat tali di gerakkan maka gelombang akan merambat dari ujung yang bebas menuju ujung yang terikat, gelombang ini disebut sebagai gelombang dating. Ketika gelombang dating tiba diujung yang terikat maka gelombang ini akan dipantulkan sehingga terjadi interferensi gelombang.
           Untuk menghitung waktu yang diperlukan gelombang untuk merambat dari titik 0 ke titik P adalah (l- x)/v . sementara itu waktu yang diperlukan gelombang untuk merambat dari titik 0 menuju titik P setelah gelombang mengalami pemantulan adalah(l+x)/v , kita dapat mengambil persamaan dari gelombang dating dan gelombang pantul sebagai berikut: 

 y₁= A sin 2π/T (t- (l-x)/v) untuk gelombang datang,

 y₂= A sin 2π/T (t- (l+x)/v+ 180⁰) untuk gelombang pantul

Keterangan:

a. Gambar pemantulan gelombang pada  ujung tali yang terikat.

b. Gambar pemantulan gelombang pada  ujung tali yang dapat bergerak bebas.

           Sehingga untuk hasil interferensi gelombang datang dan gelombang pantul di titik P yang berjarak x dari ujung terikat adalah sebagai berikut: 

y  =  y₁+ y₂

     ₌  A sin 2π (t/T - (1-x)/λ) + A sin 2π (t/T - (1+x)/λ + 180⁰) 

Dengan menggunakan aturan sinus maka penyederhanaan rumus menjadi:

sin A + sin B = 2 sin 1/2 (A+B) - cos 1/2 (A-B)

Menjadi:

y = 2A sin (2π/λ) cos 2π (t/T - 1/λ)

y = 2A sin kx (2π/T t - 2π1/λ)

Rumus interferensi

y = 2A sin kx cos (ωt - 2π1/λ)

Keterangan :

A  = amplitude gelombang datang atau pantul (m)

k  =  2π/λ

ω  = 2π/T (rad/s)

l   = panjang tali (m)

x  = letak titik terjadinya interferensi dari ujung terikat (m)

λ  = panjang gelombang (m)

t  = waktu sesaat (s)

Ap = besar amplitude gelombang stasioner (AP)

Ap = 2 A sin kx

           Jika kita perhatikan gambar pemantulan gelombang diatas , gelombang yang terbentuk adalah gelombang transversal yang memiliki bagian – bagian diantaranya perut dan simpul gelombang. Perut gelombang terjadi saat amplitudonya maksimum sedangkan simpul gelombang terjadi saat amplitudonya minimum. Dengan demikian kita akan dapat mencari letak titik yang merupakan tempat terjadinya perut atau simpul gelombang.

Tempat simpul (S) dari ujung pemantulan

S=0,1/2 λ,λ,3/2 λ,2λ,dan seterusnya

  =n (1/2 λ),dengan n=0,1,2,3,….

Tempat perut (P) dari ujung pemantulan

P= 1/4 λ,3/4 λ,5/4 λ,7/4 λ,dan seterusnya

  =(2n-1)[1/4 λ],dengan n=1,2,3,….